Байєсівська статистика та мережі Байєса
Загальний огляд
Статистику названо байєсівською на честь преподобного Томаса Байєса. Його припущення полягає в тому, що будь-яку вже відому інформацію (апріорну інформацію) може бути скомбіновано з наступним результатом вимірювання (апостеріорною інформацією), щоб установити цілковиту ймовірність. Загальний вираз теореми Байєса може бути такий:
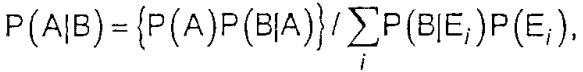
де Р(Х) — імовірність події X;
Р(Х|Y) — імовірність події X за умови, что виникла подія Y;
Еi — i-а подія.
У своїй найпростішій формі зводиться до Р(А|В) = {Р(А)Р(В|А)}/Р(В).
Байєсівська статистика відрізняється від класичної статистики тим, що вона припускає не те, що всі параметри розподілу постійні, а те, що параметри є випадковими змінними. Байєсівську ймовірність можна легше зрозуміти, якщо її розглядати як ступінь довіри особи до виникнення певної події— на відміну від класичного підходу, який базується на матеріальному свідченні подій. Оскільки підхід Байєса базується на суб'єктивному тлумаченні ймовірності, він забезпечує безпосередню основу для розглядання варіантів прийняття рішень і розробляння мереж Байєса (мереж довіри).
Метод мереж Байєса передбачає використання графічної моделі для зображення низки змінних і їхніх імовірнісних зв’язків. Мережа складається з вузлів, які представляють випадкову змінну, і стрілок, які зв’язують родинний вузол з дочірнім вузлом (родинний вузол є змінною, яка безпосередньо впливає на іншу (дочірню) змінну).
Застосування
Протягом останніх років теорія та мережі Байєса знайшли широке застосування частково завдяки їхній інтуїтивній привабливості, а також завдяки наявності відповідного обчислювального програмного забезпечення. Мережі Байєса застосовують у різноманітних сферах: медичній діагностиці, моделюванні зображень, генетиці, розпізнаванні мови, економіці, досліджуванні космосу та в сучасних потужних пошукових веб-системах. Вони можуть бути корисними в будь-якій сфері, у якій необхідно віднаходити невідомі змінні, використовуючи структурні зв’язки та дані. Мережі Байєса можна застосовувати для вивчення причинних зв’язків, щоб краще зрозуміти проблемну область і спрогнозувати наслідки втручання.
Вхідні дані
Вхідні дані подібні вхідним даним для моделювання методом Монте-Карло. Приклади етапів, які необхідно виконати для побудови мережі Байєса, такі:
- визначити змінні системи;
- визначити причинні зв'язки між змінними;
- установити умовні та апріорні ймовірності;
- додати доказове свідчення до мережі;
- актуалізувати довірчі рівні;
- виділити апостеріорні довірчі рівні.
Процес
Теорію Байєса можна застосовувати різноманітними способами. У наведеному нижче прикладі розглянуто побудову таблиці Байєса з використанням медичного тесту для визначення наявності захворювання у пацієнта. Імовірнісна довіра перед проведенням тесту полягає у тому, що 99 % популяції не мають цього захворювання, а 1 % — має (тобто це апріорна інформація). Точність тесту показала, що якщо пацієнт має захворювання, то результати тесту є позитивними у 98 % випадків. Є також імовірність того, що якщо в пацієнта немає цього захворювання, результат тесту є позитивним у 10 % випадків. У таблиці Байєса подано таку інформацію:
TODO
Вихідні дані
Підхід Байєса можна застосовувати так само, як і класичну статистику з отриманням широкого діапазону вихідних даних, наприклад, для аналізування даних з отриманням точкових оцінок і довірчих інтервалів. Широку популярність цього підходу пов’язано з застосуванням мереж Байєса для визначення апостеріорних розподілів. Графічні вихідні дані забезпечують просту для розуміння модель, а дані може бути легко змодифіковано, щоб розглядати кореляції та чутливості параметрів.
Переваги та обмеженості
| Переваги | Недоліки |
|---|---|
|
|