Марковське аналізування
Зміст
Загальний огляд
Марковське аналізування застосовують у разі, коли майбутній стан системи залежить тільки від її поточного стану. Його зазвичай застосовують до ремонтопридатних систем, які можуть перебувати в кількох станах, тобто коли аналізування надійності за блок-схемою непридатне для адекватного аналізування системи. Цей метод можна поширювати на складніші системи, застосовуючи ланцюги Маркова вищих порядків, а обмежують його лише моделі, математичне обчислення та припущення.
Марковське аналізування — кількісний метод, який може бути дискретним (з використанням імовірностей переходу з одного стану до іншого) або безперервним (з використанням швидкості переходу з одного стану до іншого).
Хоча марковське аналізування можна виконувати вручну, характер методів уможливлює використання комп’ютерних програм, більшість з яких наявні на ринку.
Застосування
Метод марковського аналізування можна застосовувати до систем з різноманітними структурами, що передбачають або не передбачають ремонтування, зокрема:
- незалежних складників, сполучених паралельно;
- незалежних складників, сполучених послідовно;
- систем з розподіленням навантаги;
- резервних систем, охоплюючи випадки, коли може виникати відмова функції перемикання;
- систем, що зазнали погіршення.
Метод марковського аналізування можна також застосовувати для обчислювання готовності, зокрема з урахуванням наявності запасних частин для ремонтування.
Вхідні дані
- Перелік різноманітних станів, у яких може перебувати система, підсистема чи складник (наприклад, стан повної працездатності, стан часткової працездатності (тобто погіршений стан), стан відмови тощо);
- Чітке розуміння можливих переходів, які необхідно змоделювати. Наприклад, погіршення стану автомобільної шини потребує врахування стану запасного колеса і, відповідно, періодичності перевіряння;
- швидкість переходу з одного стану до іншого, зазвичай подано або ймовірністю зміни станів для дискретних подій, або інтенсивністю відмов (X) і/або частотою ремонтування (р) для безперервних подій.
Процес
Основа методу марковського аналізування — концепція «станів» (наприклад, «готовність» і «відмова») і/та переходу між цими двома станами у часі за припущення постійної ймовірності змінювання стану. Використання стохастичної матриці ймовірності переходу дає змогу описувати перехід між всіма станами, уможливлюючи обчислювання різних результатів.
Щоб показати застосування методу марковського аналізування, можна розглянути складну систему, яка може перебувати тільки у трьох станах: працездатному, погіршеному та в стані відмови, означених як стани 51, 52, 53 відповідно. Кожного дня система перебуває в одному з цих трьох станів. У таблиці В.2 наведено ймовірність того, що наступного дня система перебуватиме в стані 5, де і може бути 1,2 чи 3.
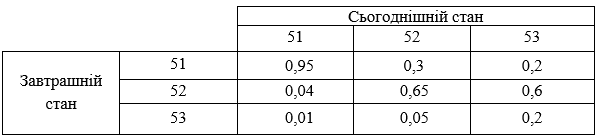
Таблиця В.2 — Матриця Маркова
Цей масив імовірностей називають матрицею Маркова чи матрицею переходу. Сума в кожному стовпці дорівнює 1, оскільки йдеться про суму всіх можливих результатів у кожному випадку. Систему можна також зобразити діаграмою Маркова, у якій кружечками є стани, а стрілками — переходи з відповідною ймовірністю (див. рисунок В.9).
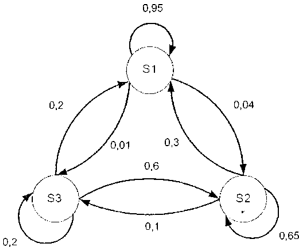
Рисунок В.9 — Приклад діаграми Маркова для стану системи
Стрілки, замкнені на одному стані, зазвичай не показують, але у цих прикладах їх наведено для повноти зображення.
Нехай Р, – імовірність перебування системи в стані / для /'=1,2,3, тоді система лінійних рівнянь, яку треба розв’язати, має такий вигляд:
P1 = 0,95P1 + 0,30P2 + 0,20P3
P2 = 0,04P1 + 0,65P2 + 0,60P3
P3 = 0,01P1 + 0,05P2 + 0,20P3
Ці три рівняння не є незалежними і не уможливлюватимуть обчислення трьох невідомих. Треба використати наведене нижче рівняння, а одне з наведених вище — вилучити.
1 = P1 + P2 + P3
Одержані значення становлять 0,85, 0,13 і 0,02 для станів 1,2, 3 відповідно. Система повністю функціює 85 % часу, перебуває в погіршеному стані протягом 13 % часу і у стані відмови — протягом 2 % часу.
Розглянемо два елементи, які функціюють паралельно, за умови, що будь-який з них має бути працездатним, щоб функціювала система. Елементи можуть перебувати або в стані працездатності, або в стані відмови, а готовність системи залежить від стану елементів.
Стани можуть бути такі:
Стан 1 — обидва елементи функціюють правильно;
Стан 2 — один елемент вийшов з ладу та його ремонтують, другий елемент функціює;
Стан 3 — обидва елементи вийшли з ладу, один з них ремонтують.
Якщо припустити, що неперервна інтенсивність відмов кожного елемента дорівнює X, а частота ремонтування дорівнює р, то діаграма переходу між станами така:
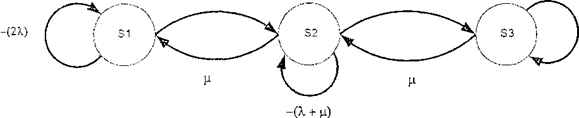
Рисунок В. 10 — Приклад діаграми переходу між станами
Неперервна інтенсивність відмов за умови переходу зі стану 1 до стану 2 становить 2Х, оскільки відмова будь-якого з двох елементів змусить систему перейти до стану 2.
Нехай Рi(t) — імовірність перебування у початковому стані та в момент часу t і Рi(t + ?t) — імовірність перебування в кінцевому стані у момент часу t + ?t. Тоді матриця ймовірностей переходу така:
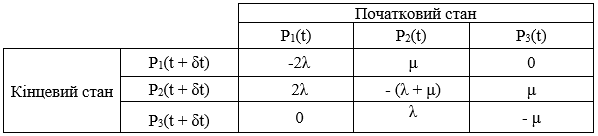
Таблица В.З — Кінцева матриця Маркова
Нульові значення виникають через неможливість переходу зі стану 1 до стану 3 або зі стану З до стану 1. Крім того, якщо визначають інтенсивність, то сума у стовпцях дорівнює нулю.
Щоб спростити обчислення, припускають, що необхідна готовність — це готовність у стабільному стані.
Вихідні дані
Вихідні дані марковського аналізування — різні ймовірності перебування в різних станах, і, таким чином, кількісна оцінка ймовірностей відмови та/чи готовності одного з основних складників системи.
Переваги та обмеженості
| Переваги | Недоліки |
|---|---|
|
|
Порівняння
Марковське аналізування нагадує аналізування мереж Петрі, оскільки уможливлює моніторинг і спостерігання за станами системи, за тієї відмінності, що мережі Петрі можуть водночас перебувати в кількох станах.
Рекомендовані документи
ІЕС 61078 Analysis techniques for dependability – Reliability block diagram and Boolean methods (Методи аналізування надійності. Блок-схема надійності та булеві методи).
ІЕС 61165 Application of Markov techniques (Застосування методів Маркова).
І5О/ІЕС 15909 (усі частини) Software and systems engineering – High-level Petri nets (Програмотехніка та системотехніка. Мережі Петрі високого рівня).